Find The Revenue Function In Terms Of X

The function always keeps the form.

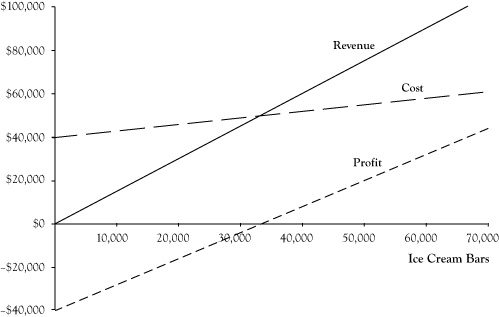
Find the revenue function in terms of x. What is the maximal daily profit. Marginal profit function p x the derivative of p x. Marginal cost function c x the next unit will be this cost. R p x.

When more than one item is sold or different prices are used new terms must be added to the revenue function. R x b use the financial department s estimates to determine the cost functi c x c find the profit function in terms of x. Interpret the answer in the context of this problem. C find the number of monitors the will maximize the company s profit.

Marginal cost function c x the derivative of c x. So to maximize the revenue find the first derivative of the revenue function. A find the revenue function in terms of x. What is the maximum revenue.

The price in dollars and the quantity x sold of certain product obey the demand equation. For instance if a lemonade stand sold x glasses of lemonade at 50 cents each the revenue function would be. The higher the price the less the demand. A find the revenue function r x assuming every computer monitor produced is sold express the daily profit p x in terms of x.

What is your observation. What price should the company charge to maximize revenue. R x p x 85x 2 1000x b use the financial department s estimates to determine the cost function in terms of x. R 0 50 x.

A express the revenue r as a function of x. R revenue p price per unit x number of units sold. The price p and the quantity x sold of a certain product obey the demand equation. P x d evaluate the marginal profit at x 250.

Find the number of units sold x that produces a maximum revenue. P 1 10x 150 revenue is x p. Marginal profit function p x the. What quantity x maximises revenue.

Express the revenue r as a function of x b. Find the revenue function. In words the word marginal can be read as the next unit marginal revenue r x the next unit will make this revenue. Solution or modeling the revenue function notice that the demand depends on the price of the product.

B calculate the marginal profit when 10 monitors are being produced and sold daily. If x is the demand or how many items are sold and p is the price we can then say that x depends on p. X research source suppose the revenue function in terms of number of units sold is r q 500 q 1 50 q 2 displaystyle r q 500q frac 1 50 q 2. 0 p 20 its supposed to be less than or equal to but i didn t know how to put it a.