Total Revenue Function R In Terms Of Q

A find the total revenue function tr q in terms of q b for what values of q.

Total revenue function r in terms of q. C f v q. Then you will need to use the formula for the revenue r x p x is the number of items sold and p is the price of one item. For the demand equation express the total revenue r as a function of the price p per item q 4p 60 also determine the price. Pages 4 this preview shows page 4 out of 4 pages.

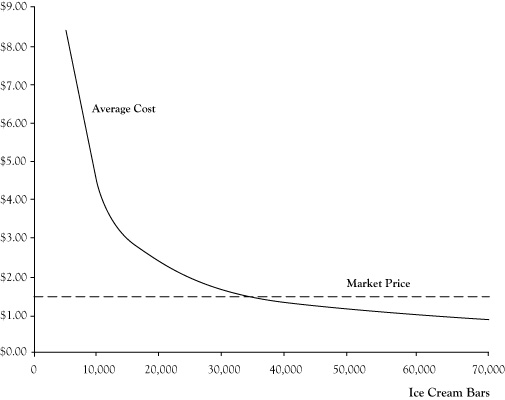
For the ice cream bar venture has two components. The cost function the sum of fixed cost and the product of the variable cost per unit times quantity of units produced also called total cost. Find the revenue function. C formulate the total profit function in terms of q.

To find the price 2. A find the total revenue function tr q in terms of q school hku. And q quantity sold per period regarding the total revenue function only in a perfectly competitive market p is obtained to be a constant independent of the firm s quantity sold q. A demand function is p 600 3q where q is the quantity of the goods sold for price p a find an expression for the total revenue r in terms of q.

Marginal revenue is the derivative of this so mr 90 4 q. R 1 5 q where r is the revenue and q is the number of units sold. B write out the total revenue function r in terms of q. A the total revenue function for this firm is tr q p q q 90 q 2 q 2.

Therefore this firm produces a quantity of 90 4 q 6 84 4 q q 21 therefore this monopoly produces a quantity of 21. However if the price is 70 dollars the demand is 5000. After some research a company found out that if the price of a product is 50 dollars the demand is 6000. A write out the total revenue function r in terms of q b write out the profit function eq pi eq in terms of q c find the output quantity q which leads to maximum profit.

However in most other types of market which would be generally called imperfectly competitive markets p depends inversely on q. Marginal cost is c 0 q 6.